Uncovering the Hidden Power of Bitwise Operators in Performance Optimization

Outcome-first introduction

You want faster loops, smaller memory footprints, and crisp, predictable integer operations in hot paths. Bitwise operators can deliver that - often with surprisingly simple code. Use them wisely, and you can make numeric truncation, modulus by powers of two, and bulk boolean storage both faster and more compact. Use them carelessly, and you’ll introduce subtle bugs when numbers overflow the 32-bit boundaries. This article shows how, when, and why to reach for bitwise tools - with practical examples and reproducible benchmarks.

Quick primer: how JavaScript treats bitwise operations

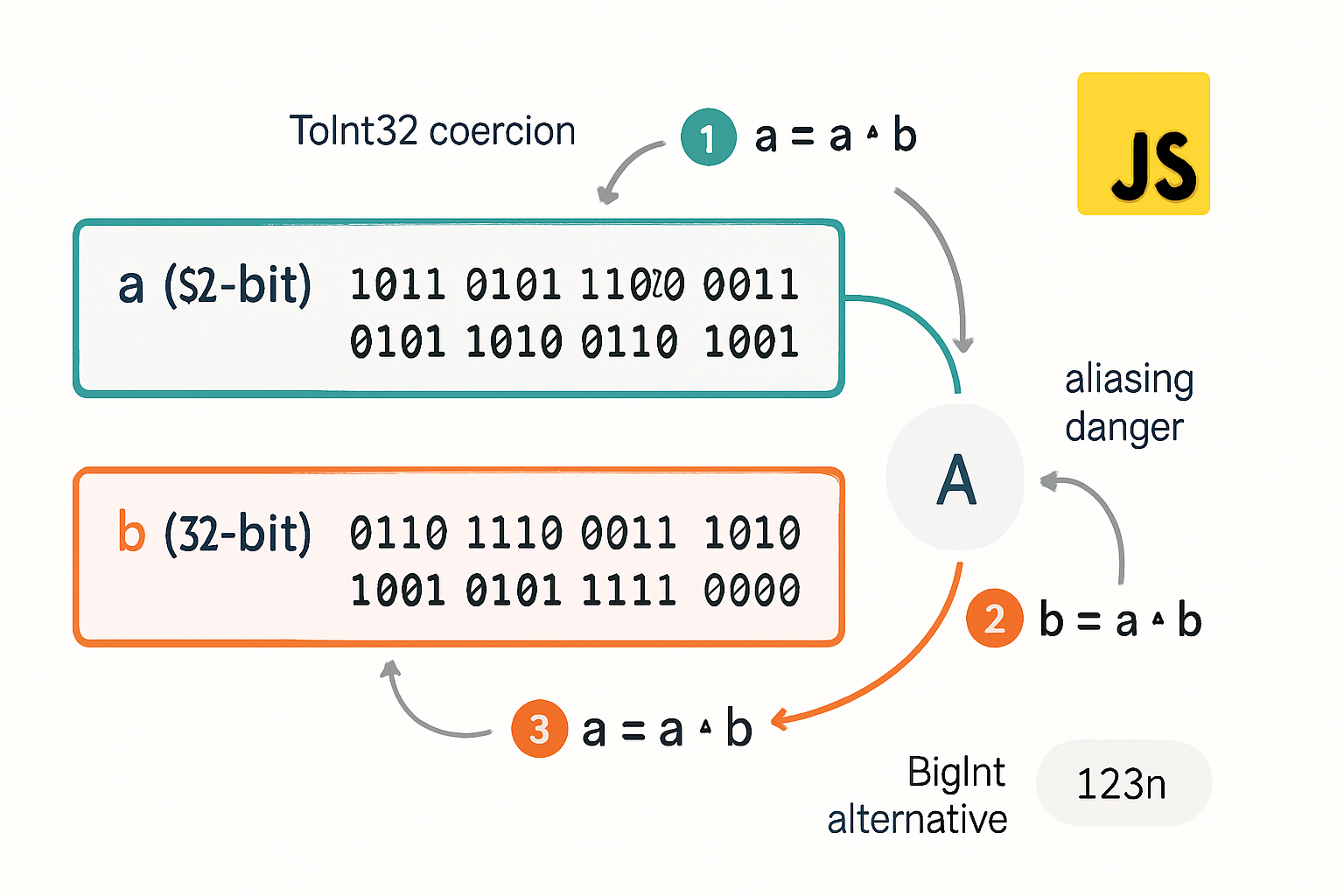
Bitwise operators in JavaScript operate on 32-bit integers. Before the CPU gets the value, JavaScript coerces numbers to a 32-bit signed integer (ToInt32). The result of the bitwise operation is then converted back to a JavaScript Number. That conversion is key: bitwise operations are fast for 32-bit integer workloads, but they lose precision above 2^31-1 (signed range: -2,147,483,648..2,147,483,647).

Convert to 32-bit signed: operations like x | 0, x >> 0, or x >>> 0 coerce values into 32-bit forms.
>>> 0 is commonly used to coerce to unsigned 32-bit (so you can treat the bits as non-negative).

Resources: MDN covers the behavior here: https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Operators/Bitwise_Operators and the ECMAScript spec describes ToInt32.

Common, practical bitwise tricks (and why they work)

Fast integer truncation (floor toward zero)

x | 0 or x >> 0 - truncate a Number to a 32-bit signed integer (floors toward zero). Useful in hot loops where you only need integer parts.

Example:

const a = 13.9;
console.log(a | 0); // 13
console.log(-13.9 | 0); // -13

Fast unsigned conversion

x >>> 0 - convert to unsigned 32-bit. Useful when you want to use bitwise masks and expect values >= 0.

const n = -1;
console.log(n >>> 0); // 4294967295

Modulo by power-of-two

x & (pow2 - 1) is equivalent to x % pow2 when pow2 is a power of two, but usually much faster and branchless.

const pow2 = 16;
const mask = pow2 - 1;
console.log(37 & mask); // 5 (37 % 16)

Even/odd check

x & 1 is a fast way to test parity.

if (x & 1) {
  /* odd */
} else {
  /* even */
}

Multiplication/division by powers of two

Shifts are multiply/divide by powers of two. But beware: right shift >> preserves sign (arithmetic shift), >>> does not (logical shift).

const doubled = x << 1; // x * 2
const half = x >> 1; // floor toward -inf for negatives, not a pure divide for floats

Packing booleans and small flags

Pack up to 32 booleans/flags in a single 32-bit integer. It reduces memory and enables very fast bulk operations (AND, OR, XOR).

let flags = 0;
const FLAG_A = 1 << 0;
const FLAG_B = 1 << 1;
flags |= FLAG_A; // set A
flags &= ~FLAG_B; // clear B
if (flags & FLAG_A) {
  /* A is set */
}

Bitsets for sets of small integers

Use a Uint32Array as an array of 32-bit buckets. Set operations (union, intersection, difference) become fast bitwise loops that are cache-friendly.

Benchmarks - how to compare (reproducible scripts)

Microbenchmarks can be misleading. But when you need to know whether a bitwise trick helps your specific workload, run a small, repeatable test. Below are two practical microbench scripts: one compares integer truncation methods; the other compares boolean-array vs bitset for population-count workloads.

Note: run these in Node.js or a browser console. Use a warmup loop. Use performance.now() (browser) or require('perf_hooks').performance in Node.

1) Truncation benchmark: Math.floor vs |0 vs ~~

// Node.js: node trunc-bench.js
const { performance } = require('perf_hooks');
const N = 5e7; // reduce if slow
const arr = new Float64Array(N);
for (let i = 0; i < N; i++) arr[i] = (Math.random() - 0.5) * 1e6;

function bench(fn, name) {
  // warmup
  for (let i = 0; i < 1e5; i++) fn(arr[i]);
  const t0 = performance.now();
  let s = 0;
  for (let i = 0; i < N; i++) s += fn(arr[i]);
  const t1 = performance.now();
  console.log(`${name}: ${(t1 - t0).toFixed(2)} ms, sum=${s}`);
}

bench(x => Math.floor(x), 'Math.floor');
bench(x => x | 0, '| 0');
bench(x => ~~x, '~~x');
bench(x => x >> 0, 'x >> 0');

// Example output (your machine may differ):
// Math.floor: 11500.48 ms, sum=...
// | 0: 4200.11 ms, sum=...
// ~~x: 4000.52 ms, sum=...
// x >> 0: 4300.77 ms, sum=...

Interpretation: historically | 0 and ~~ often run faster than Math.floor for truncation when dealing with large hot arrays. However, the difference narrows on modern engines where Math.floor is well-optimized and when the extra coercion costs matter. Always measure on your target platform.

2) Bitset vs boolean-array for counting set bits

Goal: set N booleans randomly, then count how many are true. Compare an Array of booleans vs a Uint32Array-based bitset.

// Node.js: node bitset-bench.js
const { performance } = require('perf_hooks');
const N = 1e6; // number of booleans
const TRIALS = 100;

// boolean array
const bools = new Array(N);
for (let i = 0; i < N; i++) bools[i] = Math.random() > 0.5;

// bitset using Uint32Array
const buckets = new Uint32Array(Math.ceil(N / 32));
for (let i = 0; i < N; i++) {
  if (bools[i]) buckets[i >> 5] |= 1 << (i & 31);
}

function countBools() {
  let s = 0;
  for (let i = 0; i < N; i++) s += bools[i] ? 1 : 0;
  return s;
}

// popcount using Kernighan's method
function popcount32(x) {
  x = x >>> 0;
  let c = 0;
  while (x) {
    x &= x - 1;
    c++;
  }
  return c;
}

function countBitset() {
  let s = 0;
  for (let i = 0; i < buckets.length; i++) s += popcount32(buckets[i]);
  return s;
}

// warmup
countBools();
countBitset();

let t0 = performance.now();
for (let i = 0; i < TRIALS; i++) countBools();
let t1 = performance.now();
console.log(`bools: ${(t1 - t0).toFixed(2)} ms`);

t0 = performance.now();
for (let i = 0; i < TRIALS; i++) countBitset();
t1 = performance.now();
console.log(`bitset: ${(t1 - t0).toFixed(2)} ms`);

// Example output (varies):
// bools: 320.54 ms
// bitset: 78.22 ms

Interpretation: when counting or performing set operations over many elements, a bitset reduces memory and offers much faster bitwise bulk operations. The bigger the working set, the more cache and memory-latency costs favor compact bit representations.

Real-world patterns where bitwise helps

Game loops and physics: integer ID packing, bitflags for entity states, compact component masks.
Networking: constructing protocol headers, packing small fields into 32-bit words.
Graph algorithms: adjacency bitsets for small node counts allow fast intersection operations.
Bitmap operations: collision maps, occupancy grids, and voxel occupancy where memory + bulk ops matter.

Pitfalls and things to watch out for

32-bit boundaries

Bitwise operations coerce to 32-bit signed integers. Values above 2^31-1 will wrap into negatives. If you need 64-bit integer precision, use BigInt bitwise operators or avoid bitwise ops.

Floating math semantics

Shifts and bitwise operators do not behave like pure arithmetic for negative numbers or non-integer rounding. x >> 1 is not the same as Math.floor(x / 2) for negatives. Use explicit arithmetic when semantics matter.

Readability and maintainability

Bit-twiddling can hide intent. Use clear constants and helper functions (like setFlag, clearFlag, hasFlag) to document intent.

Modern engine optimizations

Modern JS engines (V8, SpiderMonkey, JavaScriptCore) aggressively optimize common math methods. In many cases Math.floor or typed arrays with integer types are optimized enough that the raw bitwise trick no longer buys you meaningful speed. Measure before you commit.

Advanced tricks and bite-sized patterns

Rotate left / right (32-bit):

function rotl32(x, r) {
  return (x << r) | (x >>> (32 - r));
}

Fast parity / popcount improvements: precomputed lookup table for 8-bit chunks or use hardware popcount when available.
Morton codes (Z-order curve) to interleave bits for spatial indexing - implementable with bit masks and shifts.

Decision checklist - when to use bitwise

Is the operation hot (called millions of times)? Use bitwise in hot paths.
Are inputs naturally integers within 32-bit range? Safe to use bitwise.
Do you need compact storage or very fast set operations? Bitsets are excellent.
Is readability or correctness more important than micro-optimizations? Prefer clear code.

If you answered yes to the first two bullets, bitwise operators are worth profiling.

Wrap-up: practical rules

Use | 0 or ~~ for integer truncation in tight loops, but measure - Math.trunc or Math.floor may be just as fast on modern engines for your case.
Use x & (pow2 - 1) for modulus by a power-of-two.
Pack multiple flags into an integer for compactness and extremely fast boolean aggregations.
Prefer Uint32Array-backed bitsets for bulk set operations and counting.
Always test across the target runtimes and devices - micro-optimizations behave differently across engines.

Bitwise tricks are small tools with big impact when used in the right place. They give you speed and memory efficiency. But they also come with traps. Measure, document, and use them where they earn their keep.

References